(프로그래머 Lv-1) 인수의 수와 덧셈 : 인수의 수를 구하는 알고리즘

문제 설명

두 개의 정수 left그리고 right파라미터로 주어집니다. left~에서 right까지의 모든 숫자 중에서 약수가 짝수인 숫자를 더하고 약수가 홀수인 숫자가 밴 수를 반환하도록 해 함수를 완성하십시오.

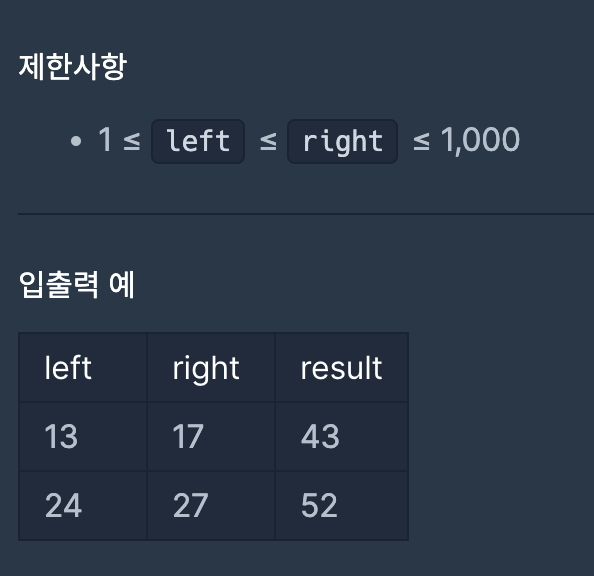
문제 해결

const solution = (left, right) => {
  let answer = 0;
    
  for (left; left < right + 1; left++) {
    if (getDivisorNum(left) % 2 === 0) {
      answer += left;
    } else {
      answer -= left;
    }
  }
  return answer;
};

function getDivisorNum(n){
    let num = 0;
    
    for (let i = 1; i * i <= n; i++) {
      if (n % i === 0) {
        num++;
        if (i * i < n) {
          num++;
        }
      }
    }
    return num;
  };

숫자 유형의 매개변수를 수신하고 숫자의 약수의 수를 반환하는 getDivisorNum 함수를 만들었습니다.

솔루션 함수는 왼쪽에서 오른쪽으로 루프에서 getDivisorNum 함수를 호출하여 제수의 수를 가져온 다음 숫자가 짝수인지 홀수인지 확인합니다.

---

약수의 수 찾기

function simpleDivisorNum (n){
	let num = 0;
    for(let i = 1; i <= n; i++){
    	if(n % i === 0){
        	num++;
        }
    }
    return num;
}

약수의 수를 찾는 간단한 방법은 각 수를 1에서 해당 수로 나누고 나머지를 확인하는 것입니다. 이 경우 시간 복잡도는 O(n)입니다.

function getDivisorNum(n){
    let num = 0;
    
    for (let i = 1; i * i <= n; i++) {
      if (n % i === 0) {
        num++;
        if (i * i < n) {
          num++;
        }
      }
    }
    return num;
  };

반면에 위의 문제를 풀기 위해 사용한 방법의 경우 시간복잡도는 O(sqrt(n))가 된다.

예를 들어, 약수 36을 찾으려면 약수는 (1, 2, 3, 4, 6, 9, 12, 18, 36)입니다.

여기에서 제수는 제곱수가 아닌 경우 항상 쌍으로 존재한다는 점에 유의해야 합니다.

(1, 36), (2, 18), (3, 12) 및 (4, 9)는 서로 쌍을 이룹니다.

6은 제곱수로 짝이 없이 홀로 존재한다.

따라서 약수를 찾으려는 숫자의 제곱근보다 작거나 같은 숫자까지만 반복하면 됩니다.

제곱근보다 작은 수가 약수인 것이 확인되면 전체 약수의 수에 2를 더한다.

확인하려는 숫자가 제곱근이면 전체 약수에 1을 더합니다.

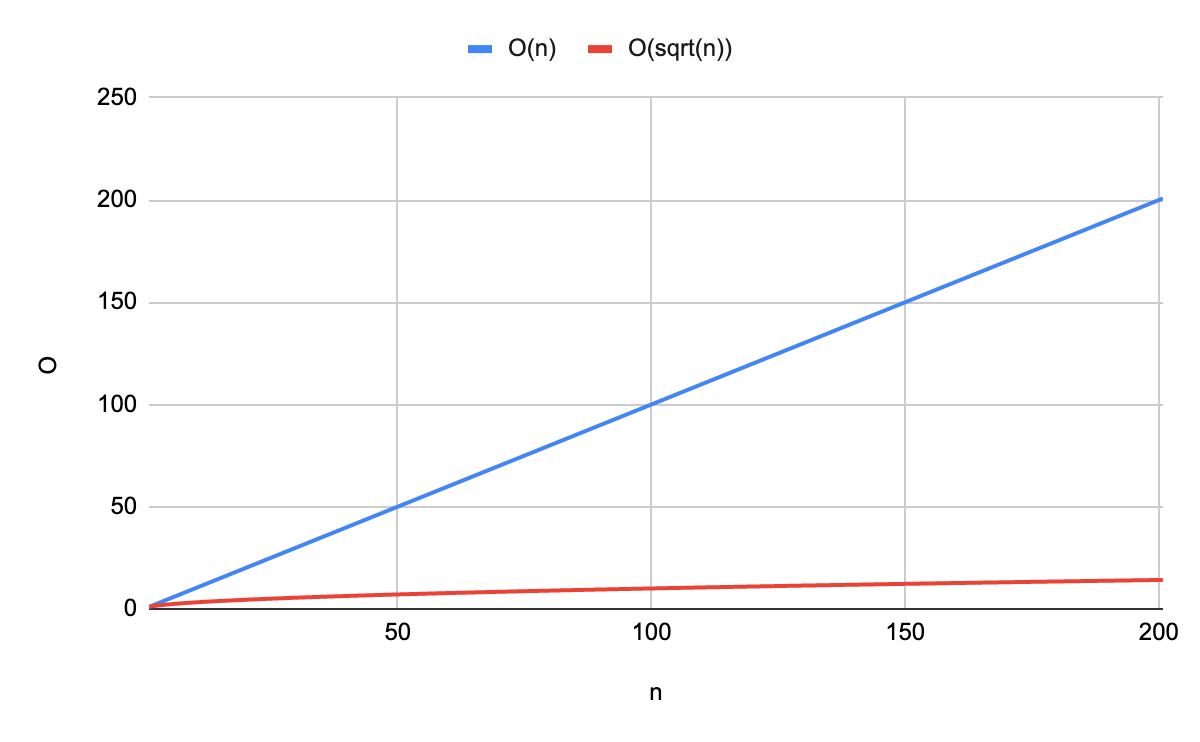
이렇게 약수의 개수를 계산할 때 시간복잡도는 O(sqrt(n))이므로 단순법보다 훨씬 간단하다.